Category: Coronapanic

“Some Countries Are Taking Social Distancing More Seriously Than Others” (Bloomberg) contains some fascinating data collected by Google. They can figure out whether or not people in any given country are naughty (not socially distant) or nice (socially distant): “In Italy, public places are a lot quieter than before the spread of coronavirus. In Sweden, they’re busier.”

Google and the journalist/editors, of course, assume that more socially distant = more righteous. More social is depicted in red and less social is depicted in green.

Sweden is just packed with covidiots milling about together and transmitting the lethal virus! But also Germany, supposedly shut down. Americans heeded the call to take to their sofas. We love to consider ourselves superior to Mexicans. And every Hollywood Democrat wants to escape Trump via emigration to Canada, not Mexico, but Mexicans have changed their behavior far more than Americans or Canadians.

Full post, including comments

How did the U.S., which spends 17 percent of GDP on health care, corresponding to every American working one day per week to pay for health care, manage to run out of capacity from a bad season of a flu-like illness?

Part of the answer is that the U.S. was never in any danger of running out of hospital capacity as a result of coronavirus, even if we had pursued a Swedish-style policy (schools, restaurants, offices open; mass gatherings shut). We have had some overcrowded hospitals, yes, but they were in all cases only a short drive away from some uncrowded hospitals. If people could wait for hours in the ED, as most did, they could easily have survived a 30-minute or 3-hour bus ride (with a nurse and maybe some oxygen bottles) to an uncrowded hospital.

See “Monroe County hospitals prepare for coronavirus ‘surge’” for example. As of March 27, when New York City was already turning into Wuhan-on-the-Hudson and three days before the USNS Comfort arrived, 33 people were hospitalized in the Rochester, NY area, which has nearly 2,000 hospital beds on a normal day as part of its state-of-the-art hospital system and top-ranked medical school. Compare to this March 25 NYT article, about patients waiting almost 60 hours for a bed at a Queens hospital. It is a 5.5-hour bus ride to Rochester. If everyone at the Queens hospital who didn’t need immediate attention had been sent to Rochester, each patient could have received personal attention from an unstressed team of physicians and nurses.

See also “During a Pandemic, an Unanticipated Problem: Out-of-Work Health Workers; Across the country, plunging revenues from canceled nonemergency medical appointments have forced hospitals to furlough or cut the pay of doctors, nurses and other staff.” (nytimes) In other words, the typical American hospital is mostly empty of both patients and staff!

New York spends $88 billion per year on its Department of Health, but apparently has put no thought into load balancing. A friend who has worked in this industry: “People in government don’t want to do anything at all until there is a disaster. Once the disaster hits, they don’t want to do anything that they haven’t already done.”

The way that the U.S. has handled coronavirus so far combines the worst features of a megasystem (huge bureaucratic costs and long bureaucratic delays) and the worst features of a small island health care system (people must be treated at the single hospital that is closest to their home).

Could it be that the most important thing we can do to prepare for the next flu-like epidemic (which might just be the next outbreak of coronavirus?) is to have some buses ready with spacious recliner chairs and oxygen bottle holders next to each chair? (Argentina already has “business class” buses like this for inter-city transport, minus the oxygen bottle holders!) Combine this with a Florida-style system for tracking hospital capacity in near real-time and we can surely expand the U.S. capability of handling epidemics by a factor of 5-10.

An Andesmar First Class bus “suite”:

Related:

• “Mayo Clinic announces sweeping pay cuts, furloughs” (MPR), from the nation’s most successful (outcomes) hospital: The state’s largest private employer is instituting across the board pay cuts and furloughs to shoulder a projected $3 billion loss this year. “The decision to eliminate elective surgeries and outpatient visits was the right decision in terms of protecting the safety of our patients and staff, and also preserving limited PPE (personal protective equipment),” said Chief Administrative Officer Jeff Bolton. “But it has led to significant reductions in revenues.” Bolton said the hospital in Rochester is at about 35 percent of capacity, while capacity in Mayo’s surgery services is at about 25 percent. “If you go back to the Great Depression, the institution went through a very similar financial crisis, and salaries were reduced during that period of time,” said Bolton. “There were a lot of actions that were very similar to the ones we are taking today.”

Full post, including comments

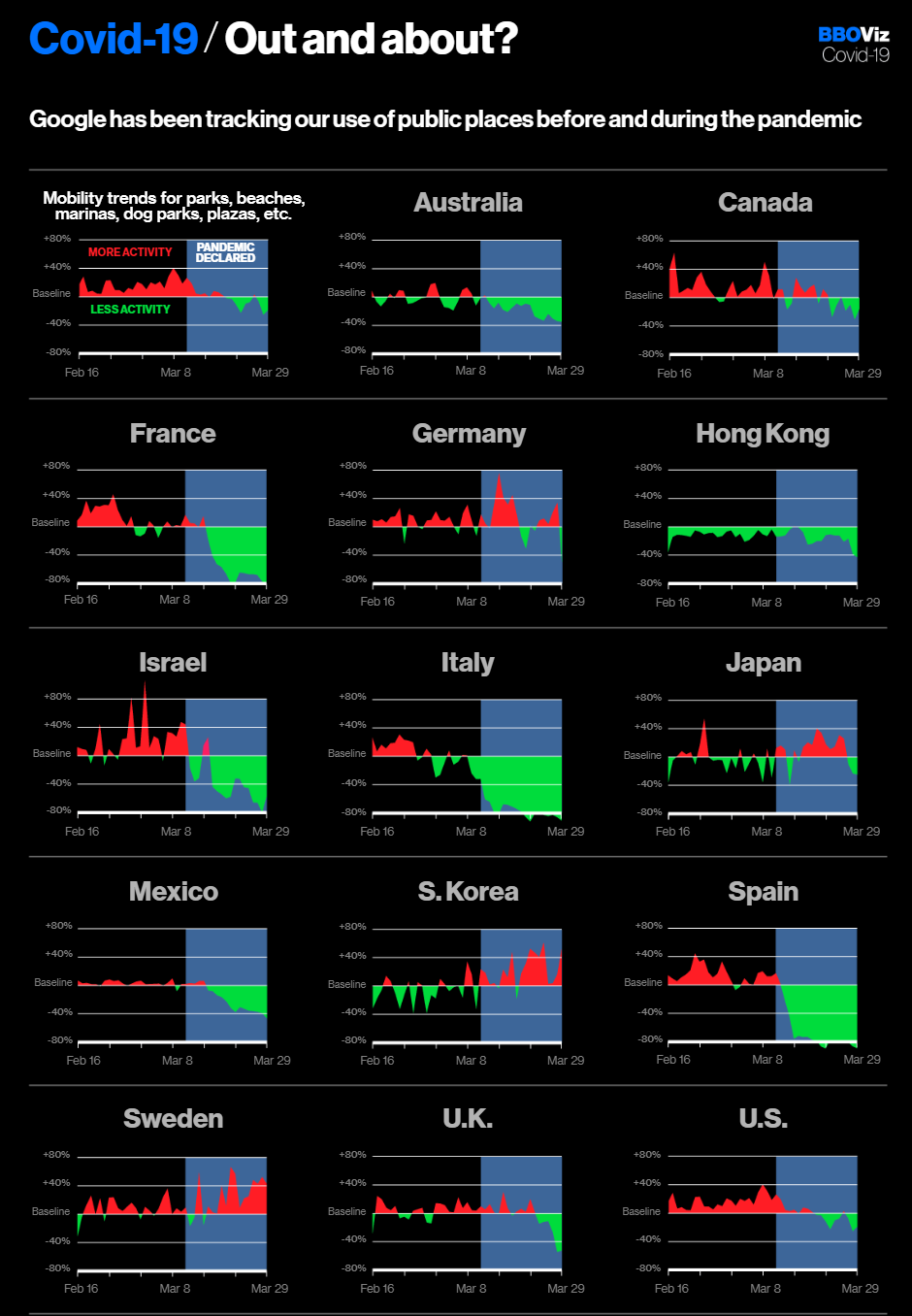
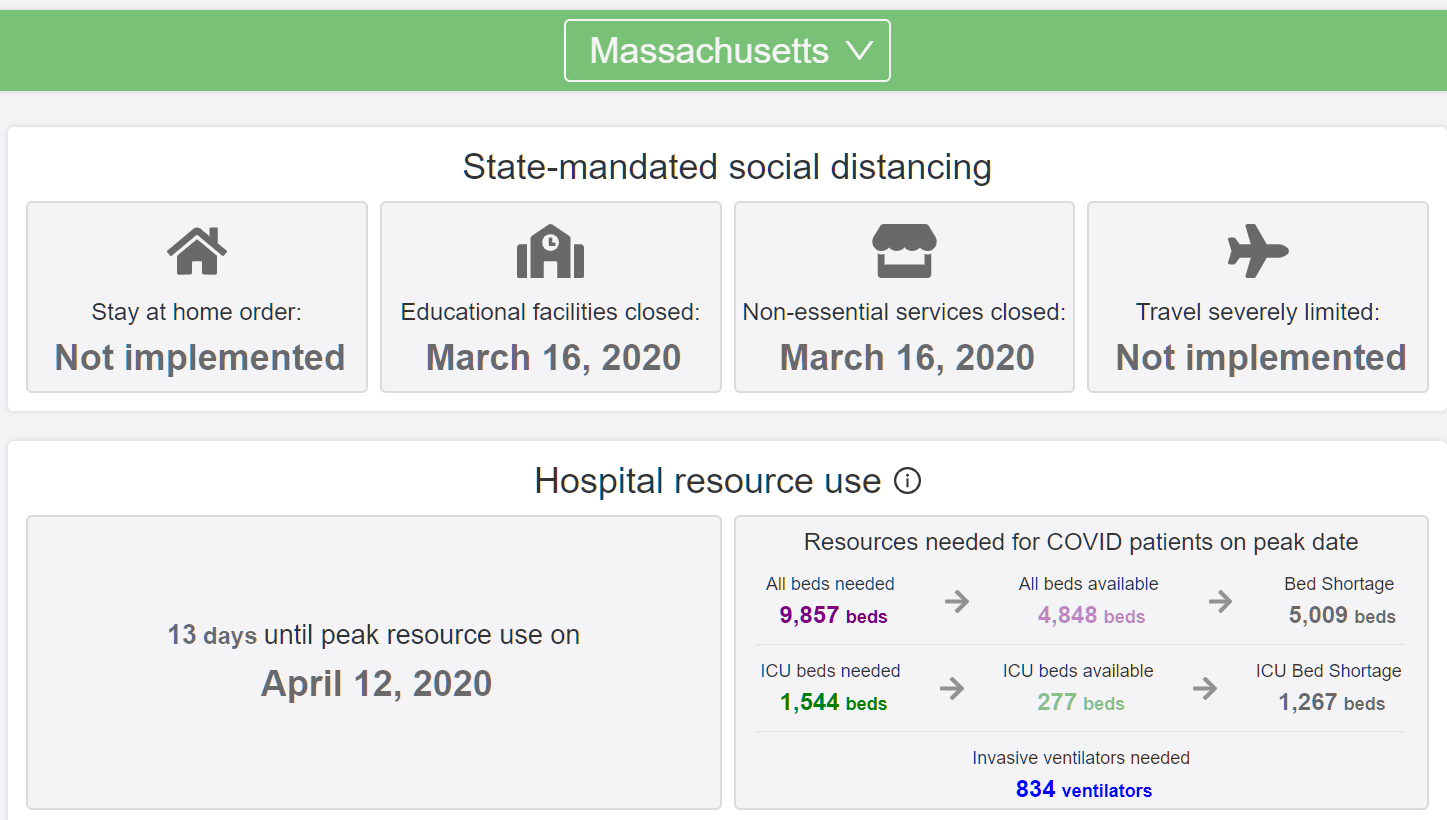
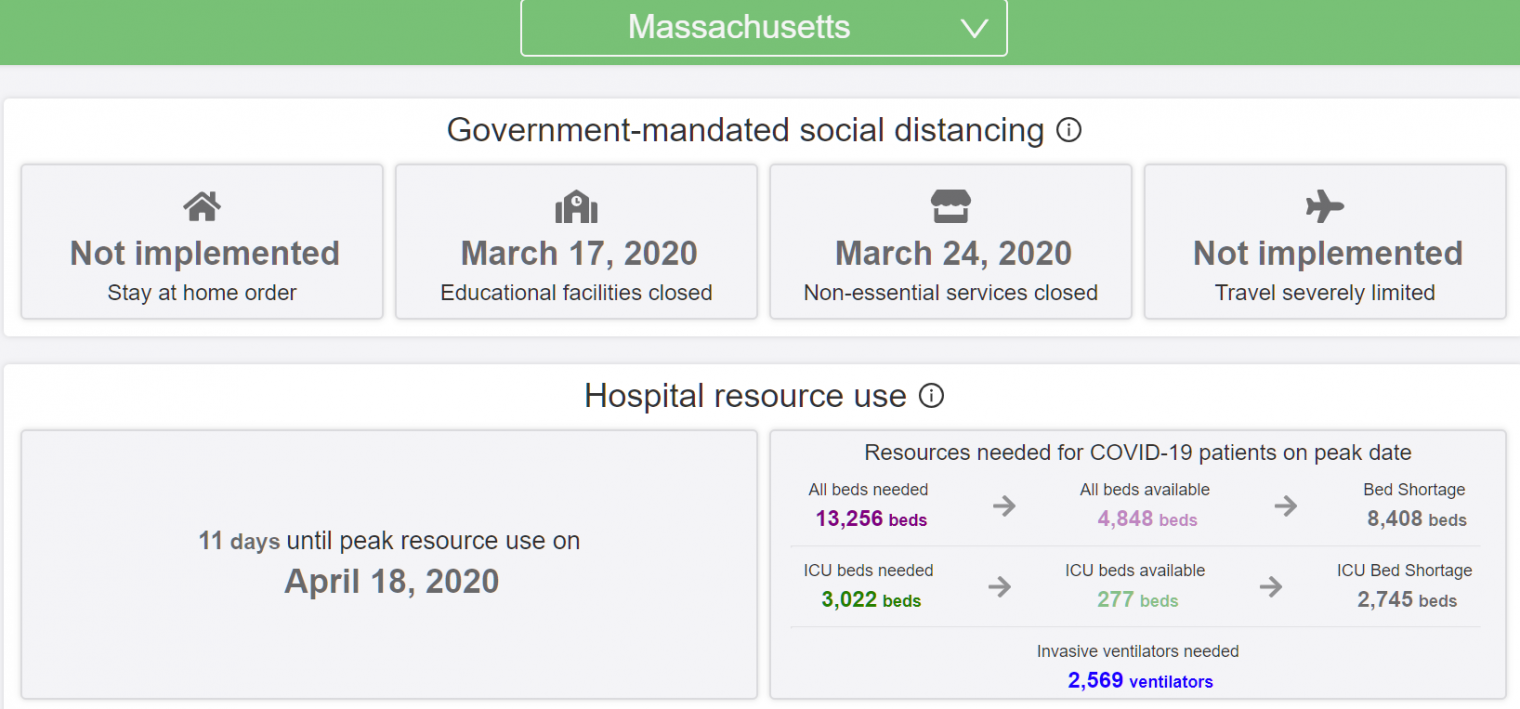
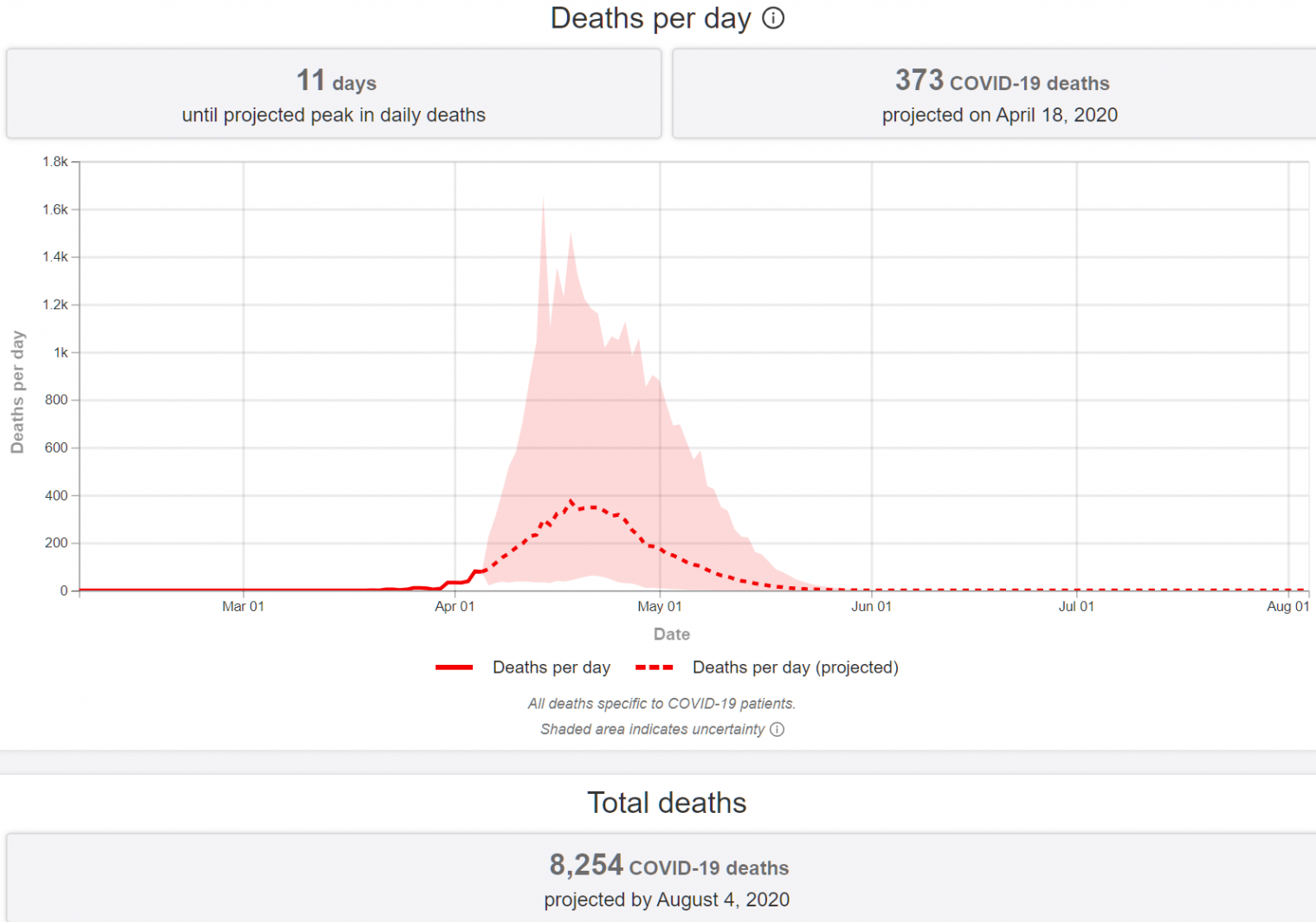
“High Contagiousness and Rapid Spread of Severe Acute Respiratory Syndrome Coronavirus 2” (preprint on cdc.gov):

Results show that the doubling time early in the epidemic in Wuhan was 2.3–3.3 days. Assuming a serial interval of 6–9 days, we calculated a median R0 value of 5.7 (95% CI 3.8–8.9).

In “Full range of coronaplague opinions” (March 25), I first noted that a team at Oxford led by Sunetra Gupta conjectured that as many as half of Britons were already infected with coronavirus due to the high R0. If the conjecture were true, it would invalidate the recommendations of the Imperial College study that led to a Western rich-country shutdown (except for Sweden). (No point in shutting down a society/economy to reduce transmission of a disease if the disease has already reached most people.)

When the Imperial College study leader upped his estimate of R0 to “just over three”, the scale of the deaths in the UK dropped by a factor of 10 (“Update on the coronapanic fueled by Imperial College”).

Can we believe this spectacular R0 number? It is lower than measles (12-18 without vaccinations). But such a high value seems inconsistent with the success of various Asian countries that have suppressed COVID-19.

Note that the authors of the new paper are huge fans of government and public health interventions:

Our results suggest that a combination of control measures, including early and active surveillance, quarantine, and especially strong social distancing efforts, are needed to slow down or stop the spread of the virus. If these measures are not implemented early and strongly, the virus has the potential to spread rapidly and infect a large fraction of the population, overwhelming healthcare systems.

But if they are right about R0, it is unclear how these could work in the U.S. once the economy and society are reopened. Consider a single infected traveler to an uninfected region of the U.S. A week after a visit to a business convention or a theatrical performance there could be more than 300 cases (45 infected at the first event, as with the choir practice in Washington; doubling to 90 after 2.5 days; doubling to 180 after 5 days; doubling to 360 after 7.5 days).

Also, if they’re right about R0, it is way too late for Sweden to do anything to change its trajectory. Our media are desperate for Swedes to die (today: “Sweden’s Relaxed Approach to the Coronavirus Could Already Be Backfiring” (TIME)), but since they didn’t shut down weeks ago the virus has to be pretty much everywhere by now. There wouldn’t be any point to Sweden falling in line with the sober non-science-denying governments.

[Note that Sweden’s new case rate is lower than Massachusetts and the death toll is similar on a population-adjusted basis (10 million for Sweden; 7 million for Massachusetts). The current University of Washington deadpool forecast is 5,625 for MA and just 4,182 for Sweden (i.e., shut-down MA will see substantially more deaths per 1,000 residents than open-for-school-and-work Sweden). Somehow the deaths of thousands of Massachusetts residents after dramatic government school and business closures is not interesting. (I’m keeping the numbers up to date in this older post.)]

Why can’t we do a test of the general population? “Coronavirus may have reached Colorado as early as January” (Colorado Sun) If R0 is, in fact, 5.7, shouldn’t everyone in Colorado who is going to develop symptoms already have developed them? (The U Washington deadpool says that Colorado peaked yesterday for hospital utilization.)

Doing a super crude calculation, in which the doubling time stays constant, we take the base 2 log of Colorado’s population of 5.6 million. From a single infected person showing up, it takes just over 22 doublings for everyone to be infected. If the doubling time is 2.5 days, that’s 55 days (i.e., if the first infected person arrived in mid-January and the doubling time lengthened gradually (due to a lot of people already being infected), the 100-percent infected time would be right around now).

Or maybe a single R0 number is not that useful. R0 is high in China and U.S. urban mass transit environments such as New York and Boston, but much lower in sprawling car-dependent environments (e.g., Denver)?

Full post, including comments

A friend has escaped with his family to Mount Desert Island, home of Acadia National Park and quiet summer playground of the rich (notably the Rockefellers). The airport was busy for a time pumping Jet A into the Gulfstreams that were dropping off elite New Yorkers fleeing Wuhan-on-the-Hudson.

If the state-by-state model is correct, those who fled to Maine made a wise choice. The state is not forecast to run out of either hospital or ICU beds (neither are neighboring New Hampshire or Vermont).

It looks as though the trails of Acadia are still open, even if the park roads and carriage roads are closed. The governor has issued a “stay at home” order, but the local sheriff says:

First and foremost, lets quash some rumors out of the gate. There are absolutely, positively NO plans to participate in random motor vehicle stops and/or check points to actively look for and arrest violators of the Governor’s order. Although this an order issued by the Governor, you retain your constitutional rights and we respect that. Please note, however, we are sworn to uphold the Constitution and laws of the State of Maine and, to that end, we are prepared to enforce the Governor’s order in the event of blatant and overtly defiant violations.

From the police log:

A Lamoine woman called the Hancock County Sheriff’s Office Monday with concerns she had about neighbors having more than 10 guests at a time at their residences despite Governor Janet Mills’ recommendation against such gatherings amid the coronavirus outbreak.

I wonder if these states break the model. As of 4/8, Vermont was supposed to have experienced peak resource demand on April 1. A total of 47 Vermonters will die, say the prophets. That’s out of a population of more than 625,000. The disease will never spread around Burlington, a reasonably dense urban environment that is packed with visitors? People who live in Southern New Hampshire often commute to plague-afflicted Boston for work. Yet the entire state is supposed to have only 66 deaths out of 1.35 million residents. The model assumes social distancing through May 2020, but the deaths are through August 4, 2020. If society reopens on June 1, won’t there be exponential growth in New Hampshire seeded from those who commute to Boston? (Even now, righteous Democrats are driving to Walmart and other places in New Hampshire so as to avoid paying sales tax here in the Land of Big Government.)

How do people in this lonely-yet-connected corner of New England escape COVID-19?

Full post, including comments

A year ago I asked, “If programmers are anti-social, how did they end up in the bustling hives of Silicon Valley?”:

People often are drawn to computer nerdism partly because they prefer interacting with machines rather than with other people. (James Damore made this point while working at Google and learned that free speech is for Americans who don’t need to work!)

Yet the coder in a modern Bay Area software plantation is sandwiched tightly between two other galley slaves (how’s that for a mixed metaphor?). He or she has less personal space than a McDonald’s cashier.

How did it come to pass that people who went into programming because they could be alone with their beloved machines are now packed like sardines into densely populated coding plantations and, after hours, packed like ocean liner steerage passengers into shared apartments?

Will this office structure, ideal for fueling any future pandemic, be reconsidered once this first wave of coronaplague subsides? Or are Silicon Valley nerds being superproductive from their cramped shared apartments such that employers won’t mind sending them into work-from-home status as soon as there is a hint of a second wave of coronaplague or whatever comes next?

Also, since people under 50 are more or less invulnerable to COVID-19 and the big Silicon Valley employers won’t hire anyone over 35, why not reopen Facebook, Google, Apple, et al? The aren’t too many senior citizens in Silicon Valley, except for some rich folks who can afford rings of servants while they keep safe in the innermost ring of their Atherton mansions.

Related:

• https://philip.greenspun.com/blog/2020/03/23/coronavirus-will-breathe-life-into-my-two-thirds-full-airline-idea/
• “What Will Tomorrow’s Workplace Bring? More Elbow Room, for Starters” (nytimes) [a coincidence; I wrote the above and scheduled it before this NYT article came out]

Full post, including comments

Back on March 29, we looked at the Massachusetts forecast for coronaplague. Science said that “Nearly as many people in Massachusetts will die as in Florida” (I forgot to write down the number) and that 3,300 Floridians would die. Massachusetts would suffer peak hospital use on April 12:

Science offers a much uglier prophecy today. Our peak is due on April 18, 2020 (another week of suffering and nail-biting). A shocking 8,254 of us will die (out of 7 million). That’s a higher per capita rate than what New York (15,618 deaths out of a population of 20 million) will suffer and more than Florida (forecast at 6,770). The forecast for the entire country remains roughly constant at 81,766. We have less than 10 percent of the ICU beds that we need and only about one third as many hospital beds. In other words, if you’re not crazy you’d be getting into a car right now and driving to Tennessee or Texas (both forecast to have few deaths per capita and no shortage of health care resources; Steve Jobs chose to get all of his cancer care in Memphis, ultimately).

Bad news:

Worse news:

One thing that is very odd is the counting of deaths. In “Number of new COVID-19 cases worldwide is declining now?” I link to the official state reports of deaths. The forecast says that there were “78 deaths per day” (actual) on April 5, 2020. The New York Times today says that we have suffered only 154 deaths total in the greater Boston area (includes southern NH); worldometers says 260 total deaths so far in Massachusetts (I have a tough time believe many are occurring outside of the greater Boston area). The latest report from the state, which includes some deaths from over the weekend (apparently there is a reporting lag) says 356 people have died thus far, so maybe the correct data are being fed into the model.

It doesn’t look as though the U.S. as a nation will run out of health care resources to supply every COVID-19 patient with whatever the state-of-the-art therapy is (i.e., not much that is useful right now). However, since there is no load-balancing system for sending patients to idle hospitals, even within a city or state, some places seem to be at risk of dire Fall of Saigon-style situations. Massachusetts appears to be one of the worst prepared states, on the same scale as New York, but without the military support of a field hospital or a hospital ship.

[What about our shutdown? We’ve closed our schools, restaurants, and stores (except for marijuana and liquor). What did that do for us? The model site forecasts 4,182 deaths for Sweden (population 10 million; not shut down) and 8,254 for Massachusetts (population 7 million; shut down). I.e., we’re almost 3X as likely to die while alone at home watching Netflix compared to a Swede who is out eating and drinking with his/her/zer/their friends.]

Full post, including comments

I’m a big believer that viruses are smarter than human beings. We haven’t been able to do anything about the common cold (nearly 1 billion cases per year in the U.S.), despite the enormous economic rewards waiting for anyone who can come up with a real therapy. We have no treatment for SARS or MERS despite recognizing the terrifying potential of these diseases. Tamiflu doesn’t stop the flu from killing people.

A smart numbers-oriented friend points out, however, that we have a lot more clinical data regarding COVID-19 than we did for SARS (8,000 cases) and MERS (a handful). He believes that we’ll therefore be able to emerge from our suburban bunkers relatively soon and actually be treated for COVID-19 (as opposed to being parked on a ventilator so that we can die with 86% probability at a slightly later date).

Keeping in mind that it took months for coronavirus tests to be invented, approved, and manufactured (still not in sufficient quantities except for those who are hospitalized), what’s your best guess as to when you can go into the hospital ED, have the nurse shout out “COVID-19” and then an assistant comes in with some pills or a shot that will keep the symptoms down to some reasonable level of misery?

My guess: between July 2020 and March 2021, with October 2020 as the best single month guess.

Related:

• “Why the coronavirus and most other viruses have no cure” (Philadelpia Inquirer)

Full post, including comments

One of my flying connections co-owns five liquor stores (“package stores” in the local argot) here in the Boston area. His family has been doing this for four generations, which tells you how profitable it is during ordinary times.

How’s business? “We’re up 50 percent since the shutdown,” he said. “The main challenge is getting staff to come in. We’ve put in Plexiglas dividers and cut down on the number of shift changes. We sanitize between every shift, but they’re still afraid.” Was he forced to raise wages? “We gave every salaried employee a 25 percent bonus and are paying the part-timers time and a half.”

I wonder if more Massachusetts residents will die from alcoholism in the years following this shutdown than were saved (if any were saved) by spreading COVID-19 infections over an extra few weeks.

Some recent photos from a walk around Cambridge…

The Black Death caused some people to abandon religion, but Rainbow Flagism has not visibly suffered yet:

• 

• 

The local church:

• 

• 

This gathering place is closed:

• 

• 

Some traditions cannot be abandoned:

In response to demands from the young and mostly invulnerable to COVID-19, I boiled some water and flattened the curve on this linguini:

Watched Fox News. Believed Trump. His personal curve was flattened. RIP. #SidewalkCoronaVictim

Full post, including comments